गति के नियम

गति के दूसरे नियम की गणितीय गणना

मान लीजिए कि m द्रव्यमान वाली कोई वस्तु आरंभिक वेग u से चल रही है। वस्तु पर जब t सेकंड के लिए F बल लगाया जाता है तो वस्तु की गति बदलकर v हो जाती है।

वस्तु का प्रारंभिक संवेग `=p_1=mu`

वस्तु का अंतिम संवेग `=p_2=mv`

संवेग में परिवर्तन `∝p_2-p_1`

`∝mv-mu`

संवेग परिवर्तन की दर `∝(mv-mu)/t`

`∝(m(v-u))/t`

या लगाया गया बल `F∝(m(v-u))/t`

हम जानते हैं कि `(v-u)/t=a`

इसलिए `F∝ma`

या `F=km\a`

यहाँ पर एक आनुपातिकता का स्थिरांक है। यदि का मान इकाई है तो

`F=ma`

इस तरह से बल का मात्रक किग्रा मी प्रति वर्ग (Kg m s^-2) सेकंड है। बल के मात्रक को सर आइजैक न्यूटन के सम्मान में न्यूटन कहा जाता है।

उदाहरण: जब क्रिकेट के किसी फील्डर के पास बॉल तेजी से आती है तो बॉल को पकड़ते समय वह अपने हाथों को थोड़ा पीछे की ओर खींच लेता है। इससे बॉल के संवेग को शून्य करने के लिए अतिरिक्त समय मिल जाता है। इससे खिलाड़ी को चोट लगने की संभावना कम हो जाती है। यदि फील्डर अचानक से गेंद को पकड़ेगा तो उसकी हथेलियों में बहुत चोट लगेगी।

उदाहरण: लॉन्ग जम्प और हाई जम्प के खिलाड़ी जहाँ पर लैंड करते हैं वहाँ पर गद्दा या रेत को रखा जाता है। इससे संवेग को शून्य करने के लिए अतिरिक्त समय मिल जाता है और खिलाड़ी को घायल होने से बचाया जा सकता है।

गति के दूसरे नियम के समीकरण से गति के पहले नियम को भी समझा जा सकता है।

`F=ma`

या `F=(m(v-u))/t`

या `F=(mv-mu)/t`

या `Ft=mv-mu`

अगर F = 0 होगा तो v = u यानि वस्तु जिस गति से चल रही है उसी गति से चलती रहेगी। यदि u = 0 तो v = 0 होगा यानि वस्तु अगर विराम अवस्था में रहेगी तो गति में नहीं आयेगी।

गति का तीसरा नियम

किसी भी क्रिया के लिए ठीक उसके समान और उसकी विपरीत दिशा में प्रतिक्रिया होती है। यानि सब आप किसी वस्तु पर कोई बल लगाते हैं तो वह वस्तु समान बल उसकी विपरीत दिशा में लगाती है। यदि आप दीवार पर मुक्का मारते हैं तो दीवार समान बल से प्रतिक्रिया करती है। इसलिए जोर से मुक्का मारने पर दीवार से आपको चोट भी लग सकती है।

यह याद रखने की बात है कि हालाँकि क्रिया और प्रतिक्रिया समान मात्रा में होती है लेकिन दोनों से उत्पन्न होने वाला त्वरण समान नहीं हो सकता है। इसके लिए बंदूक से छूटने वाली गोली का उदाहरण लेते हैं। जब गोली छूटती है तो उसपर एक नियत बल लगता है। गोली उसी मात्रा में बंदूक पर बल लगाती है। गोली का द्रव्यमान कम होने के कारण गोली का त्वरण अधिक होता है और वह तेज गति से आगे बढ़ती है। गोली की तुलना में बंदूक का द्रव्यमान बहुत अधिक होता है इसलिए बंदूक का त्वरण बहुत कम होता है। इसलिए बंदूक पीछे की ओर खिसकती तो है लेकिन बहुत ही कम गति से।

संवेग संरक्षण

मान लीजिए कि दो गेंदें A और B हैं जिनके द्रव्यमान क्रमश: m_A और m_B हैं तथा उनके वेग u_A और u_B हैं। मान लीजिए कि u_A > u_B है। दोनों गेंदें एक ही रेखा में गमन कर रही हैं और तथा में टक्कर होती है। ऐसे A में द्वारा B पर लगाया गया बल F_AB है और B द्वारा A पर लगाया गया बल F_BA है।

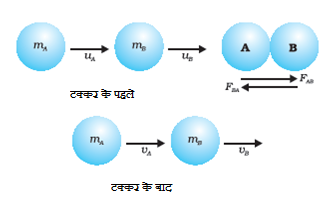
टक्कर के पहले गेंद A का संवेग = m_Au_A

टक्कर के बाद गेंद A का संवेग = m_Av_A

गेंद A में संवेग परिवर्तन की दर `=F_(AB)=(m_A(v_A-u_A))/t`

टक्कर के पहले गेंद B का संवेग = m_Bu_B

टक्कर के बाद गेंद B का संवेग = m_Bv_B

गेंद B में संवेग परिवर्तन की दर `=F_(BA)=(m_B(v_A-u_B))/t`

गति के तीसरे नियम के अनुसार, गेंद A द्वारा लगाये बल की मात्रा गेंद B द्वारा लगाया गये बल के समान होगी और विपरीत दिशा में होगी।

F_AB = - F_BA

या `(m_A(v_A-u_A))/t=-(m_B(v_B-u_B))/t`

या `m_A(v_A-u_A)=-m_b(v_B-u_B)`

या `m_Av_A-m_Au_A = -m_Bv_B+m_Bu_B`

या `m_Au_A+m_Bu_B=m_Av_A+m_Bv_B`

इससे पता चलता है कि टक्कर के पहले का कुल संवेग और टक्कर के बाद का कुल संवेग बराबर होगा। इसका मतलब यह हुआ कि जब कोई बाहरी बल काम नहीं करता है तो गेंदों का कुल संवेग संरक्षित रहता है। इसे संवेग संरक्षण का नियम कहते हैं। दो वस्तुओं का कुल संवेग टकराने की प्रक्रिया में नहीं बदलता है यानि संरक्षित रहता है।