ज्यामितीय संरचनाएँ

अभ्यास 11.1 Part 1

प्रश्न 1: 7.6 सेमी लंबा एक रेखाखंड खींचिए और इसे 5:8 के अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।

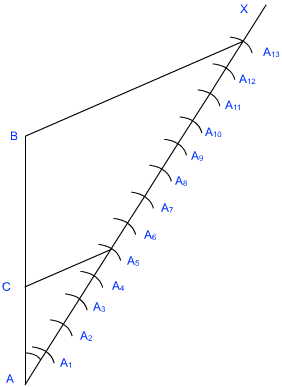
उत्तर: एक रेखाखंड खींचिए AB = 7.6 cm.

एक किरण AX खींचिए जो AB के साथ न्यूनकोण बनाती हो।

अब AX पर 13 बिंदु (5 + 8) A₁, A₂, A₃, …….A₁₃ बनाइए ताकि:

AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇ = A₇A₈ = A₈A₉ = A₉A₁₀ = A₁₀A₁₁ = A₁₁A₁₂ = A₁₂A₁₃

अब A₁₃ को B से मिलाइए।

बिंदु A₅, से एक रेखा A₅C || A₁₃B; खींचिए जो AB को बिंदु C काटती है।

यहाँ पर, AC : CB = 5 : 8

AC = 2.92 cm और CB = 4.68 cm

प्रश्न 2: 4 सेमी, 5 सेमी और 6 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की `2/3` गुनी हों।

उत्तर: त्रिभुज का निर्माण:

• एक रेखाखंड AB = 4 cm खींचिए
• बिंदु A से 5 सेमी की दूरी पर एक चाप खींचिए।
• बिंदु B से 6 सेमी की दूरी पर एक चाप खींचिए जो पिछले चाप को काटता हो।
• अब इस प्रतिच्छेद बिंदु को A और B से मिलाइए।
• इससे त्रिभुज ABC बनता है।

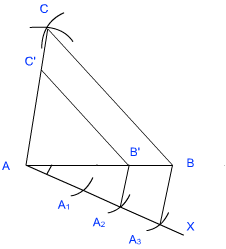
आधार को 2 : 3 के अनुपात में बाँटना:

• एक किरण AX खींचिए जो AB के साथ न्यूनकोण बनाती है।
• अब AX पर तीन बिंदु डालिए ताकि AA₁ = A₁A₂ = A₂A₃
• अब A₃ को B से मिलाइए।
• बिंदु A₂ से एक रेखा खींचिए ताकि यह A₃B के समांतर हो और AB को बिंदु B’ पर काटती हो।
• बिंदु B’ से एक रेखा खींचिए जो BC के समांतर हो और AC बिंदु C’ पर काटती हो।

इससे त्रिभुज AB’C’ बनता है।

प्रश्न 3: 5 सेमी, 6 सेमी और 7 सेमी भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिये हुए त्रिभुज की संगत भुजाओं की `7/5` गुनी हों।

उत्तर: त्रिभुज का निर्माण:

• एक रेखाखंड AB = 5 cm खींचिए।
• Draw an arc at 6 cm from point बिंदु A से 6 सेमी की दूरी पर एक चाप खींचिए।
• बिंदु B से 7 सेमी की दूरी पर एक चाप खींचिए जो पिछले चाप को काटता हो।
• प्रतिच्छेद बिंदु को A और B से मिलाइए।
• इससे त्रिभुज ABC बनता है।

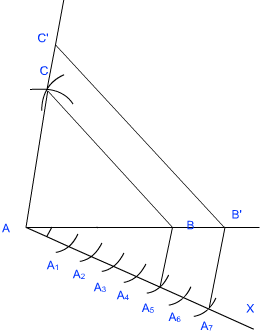
आधार का विभाजन:

• एक किरण AX खींचिए जो AB के साथ न्यूनकोण बनाता है।
• बिंदु AX पर 7 बिंदु बनाइए ताकि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇.
• अब A₅ को B से मिलाइए।
• बिंदु A₇ से एक रेखा खींचिए जो A₅B के समांतर हो और AB’ से मिलती हो (AB को AB’ तक बढ़ाया गया है)
• एक रेखा B’C’ || BC खींचिए।

इससे त्रिभुज AB’C’ बनता है।