संख्या पद्धति
अभ्यास 1.4
प्रश्न 1: उत्तरोत्तर आवर्धन करके संख्या रेखा पर 3.765 को देखिए।
उत्तर: एक संख्या रेखा खींचिए
इस रेखा पर 3 और 4 के बीच के स्थान का आवर्धन करके उसे 10 बराबर हिस्सों में बाँटिए।
अब 3.7 और 3.8 के बीच के हिस्से का आवर्धन करके उसे 10 बराबर हिस्सों में बाँटिए।
अब 3.765 को चिह्नित कीजिए।
पहला आवर्धन

दूसरा आवर्धन

तीसरा आवर्धन
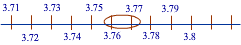
चौथा आवर्धन
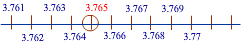
प्रश्न 2: 4 दशमलव स्थानों तक संख्या रेखा पर 4.26 को देखिए।
उत्तर: एक संख्या रेखा लीजिए
इस रेखा पर 4 और 5 के बीच के हिस्से का आवर्धन करके उसे 10 बराबर हिस्सों में बाँटिए।
अब 4.2 और 4.3 के बीच के हिस्से का आवर्धन करके उसे 10 बराबर हिस्सो में बाँटिए।
अब 4.26 और 4.27 के बीच के हिस्से को 10 बराबर भागों में बाँटिए।
अब 4.262 और 4.263 के बीच के हिस्से को 10 बराबर भागों में बाँटिए।
अब 4.2626 को चिह्नित कीजिए।
पहला आवर्धन
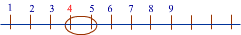
दूसरा आवर्धन

तीसरा आवर्धन

चौथा आवर्धन
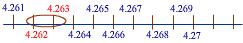
पाँचवा आवर्धन
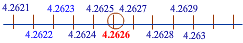
अभ्यस 1.5
प्रश्न 1: बताइर नीचे दी गई संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैं:
- `2-sqrt5`
- `(3+sqrt(23))-sqrt(23)`
- `(2sqrt7)/(7sqrt7)`
- `1/(sqrt2)`
- π
उत्तर: (a) अपरिमेय, (b) परिमेय, (c) परिमेय, (d) अपरिमेय, (e) अपरिमेय
प्रश्न 2: निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए:
(a) `(3+sqrt3)(2+sqrt2)`
उत्तर: दिया गया है, `(3 + sqrt3)(2 + sqrt2)`
`= 3 xx 2 + 2sqrt3 + 3sqrt2 + sqrt3 xx\ sqrt2`
`= 6 + 2sqrt3 + 3sqrt2 + sqrt6`
(b) `(3+sqrt3)(3-sqrt3)`
उत्तर:
दिया गया है, `(3 + sqrt3)(3 - sqrt3)`
= (चूँकि, `(a + b)(a – b) = a^2 – b^2`
इसलिए, `3^2 – (sqrt3)^2`
`= 9 – 3 = 6`
(c) `(sqrt5+sqrt2)^2`
उत्तर: दिया गया है `(sqrt5 + sqrt2)^2`
(चूँकि, `(a + b)^2 = a^2 + b^2 + 2ab`
इसलिए; `(sqrt5)^2 + (sqrt2)^2 + 2 xx sqrt5 xx sqrt2`
`= 5 + 2 + 2sqrt10`
`= 7 + 2sqrt10`
(d) `(sqrt5-sqrt2)(sqrt5+sqrt2)`
उत्तर: दिया गया है, `(sqrt5 - sqrt2)( sqrt5 + sqrt2)`
(चूँकि, `(a + b)(a – b) = a^2 – b^2`
इसलिए, `(sqrt5)^2 – (sqrt2)^2 = 5 – 2 = 3`
प्रश्न 3: आपको याद होगा कि π को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिए d) के अनुपात से परिभाषित किया जाता है, अर्थात `π=c/d` है। यह इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे?
उत्तर: जब आप एक पैमाने से किसी लम्बाई को मापते हैं तो आपको केवल एक प्रमेय मान मिलता है जो वास्तविक लम्बाई के लगभग बराबर होता है। इसलिए आपको यह नहीं मालूम होता है कि परिधि और व्यास में से किसका मान अपरिमेय है। इसलिए यहाँ पर कोई अंतर्विरोध नहीं है।
प्रश्न 4: संख्या रेखा पर `sqrt(9.3)` को निरूपित कीजिए।
उत्तर: एक क्षैतिज रेखा खींचिए और उस पर 9.3 इकाई का रेखाखंड CA खींचिए।
अब AB = 1 लीजिए
अब CB का मध्य बिंदु चिह्नित कीजिए जो कि O है।
OB को त्रिज्या मानते हुए एक अर्धवृत्त बनाइए।
बिंदु A पर एक लम्ब खींचिए जो अर्धवृत्त को बिंदु D पर काटता है।
AD का मान `sqrt(9.3)` है।
एक कम्पास से AD का माप लीजिए और फिर उसके बराबर एक क्षैतिज रेखा खींचिए जो बिंदु A से निकलकर बिंदु E पर मिलती है।
यहाँ AD = AE = `sqrt(9.3)`
प्रश्न 5: निम्नलिखित के हरों का परिमेयकरण कीजिए:
(a) `1/(sqrt7)`
उत्तर: `=(1/sqrt7)xx(sqrt7/sqrt7)`
`=(1xxsqrt7)/(sqrt7xxsqrt7)=(sqrt7)/7`
(b) `1/(sqrt7-sqrt6)`
उत्तर: `1/(sqrt7-sqrt6)`
`=(1/(sqrt7-sqrt6))xx((sqrt7+sqrt6)/(sqrt7+sqrt6))`
`(sqrt7+sqrt6)/((sqrt7-sqrt6)(sqrt7+sqrt6))`
Since, `a^2-b^2=(a+b)(a-b)`
So, we have, `(sqrt7+sqrt6)/((sqrt7)^2-(sqrt6)^2)`
`=(sqrt7+sqrt6)/(7-6)`
`(sqrt7+sqrt6)/1=sqrt7+sqrt6`
(c) `1/(sqrt5+sqrt2)`
उत्तर: `1/(sqrt5+sqrt2)`
`=(1/(sqrt5+sqrt2))xx((sqrt5-sqrt2)/(sqrt5-sqrt2))`
`(sqrt5-sqrt2)/((sqrt5+sqrt2)(sqrt5-sqrt2))`
`=(sqrt5-sqrt2)/((sqrt5)^2-(sqrt2)^2)`
`=(sqrt5-sqrt2)/(5-2)=(sqrt5-sqrt2)/3`
उत्तर: `1/(sqrt7-2)`
`=(1)/(sqrt7-2)xx(sqrt7+2)/(sqrt7+2)`
`=(sqrt7+2)/((sqrt7)^2-2^2)`
`=(sqrt7+2)/(7-4)=(sqrt7+2)/3`
अभ्यास 1.6
प्रश्न 1: ज्ञात कीजिए:
(a) `64^(1/2)`
उत्तर: `64^(1/2)`
`=(8xx8)^(1/2)=(8^2)^(1/2)`
`=8^(2xx1/2)=8^1=8`
(b) `32^(1/5)`
उत्तर: `32^(1/5)`
`=(2xx2xx2xx2xx2)^(1/5)`
`=2^(5xx1/5)=2^1=2`
(c) `125^(1/3)`
उत्तर: `125^(1/3)`
`=(5xx5xx5)^(1/3)`
`=(5^3)^(1/3)=5^1=5`
प्रश्न 2: ज्ञात कीजिए:
(a) `9^(3/2)`
उत्तर: `9^(3/2)`
`=(3^2)^(3/2)`
`=3^(2xx3/2)=3^3=27`
(b) `32^(2/5)`
उत्तर: `32^(2/5)`
`=(2xx2xx2xx2xx2)^(2/5)`
`=(2^5)^(2/5)=2^(5xx2/5)=2^2=4`
(c) `16^(3/4)`
उत्तर: `16^(3/4)`
`=(2xx2xx2xx2)^(3/4)`
`=(2^4)^(3/4)=2^(4xx3/4)=2^3=8`
(d) `125^(-1/3)`
उत्तर: `125^(-1/3)`
`=(5xx5xx5)^(-1/3)`
`=(5^3)^(-1/3)=5^(3xx-1/3)=5^-1=1/5`
प्रश्न 3: सरल कीजिए:
(a) `2^(1/3)`, `2^(1/5)`
उत्तर: `2^(2/3).2^(1/5)`
चूँकि, `a^m.a^n=a^(m+n)`
`=(2)^(2/3+1/5)=(2)^((10+3)/15)=2^(13/15)`
(b) `(1/(3^3))^7`
उत्तर: `(1/(3^3))^7`
`=(3^-3)^7=3^(-3xx7)=3^-21`
(c) `(11^(1/2))/(11^(1/4))`
उत्तर: `(11^(1/2))/(11^(1/4))`
`=(11)^(1/2-1/4)=(11)^((2-1)/4)=11^1/4`
(d) `7^(1/2)`, `8^(1/2)`
उत्तर: `7^(1/2).8^(1/2)`
हम जानते हैं, `a^m.b^m=(ab)^m`
`=(7xx8)^(1/2)=56^(1/2)`