वृत्त

अभ्यास 6

Part 2

प्रश्न 6: ABCD एक समांतर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।

उत्तर: इस आकृति में समांतर चतुर्भुज ABCD दिखाया गया है। एक वृत्त A,B और C से होकर गुजरता है लेकिन CD को बिंदु E पर काटता है।

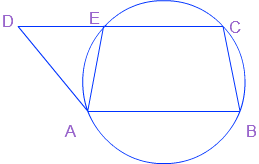
चूँकि, ABCE एक चक्रीय चतुर्भुज है

इसलिए, ∠AEC + ∠B = 180° …………………..(1)

ABCD एक समांतर चतुर्भुज है

इसलिए, ∠D = ∠B ……………..(2) (समांतर चतुर्भुज के सम्मुख कोण)

समीकरण (1) और (2) से

∠AEC + ∠D = 180° ……………………….(3)

लेकिन ∠AEC + ∠AED = 180° (कोणों के रैखीय युग्म) …………………… (4)

समीकरण (3) और (4) से

∠D = ∠AED

इसका मतलब है ΔADE के आधार पर के कोण बराबर हैं

इसलिए, AE = AD (समान कोणों के सामने की भुजाएँ)

प्रश्न 7: AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए

(a) AC और BD व्यास हैं
(b) ABCD एक आयत है।

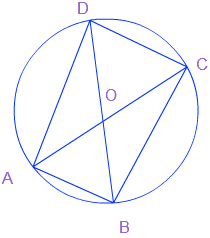
उत्तर: इस आकृति में एक वृत्त को दिखाया गया है जिसकी जीवाएँ AC और BD एक दूसरे को बिंदु O पर काटती हैं।

सिद्ध करना है: (i) AC और BD व्यास है और (ii) ABCD एक आयत है

निर्माण: AB, BC, CD और DA को जोड़ें

प्रमाण: (i) ΔAOB और ΔCOD में

AO = CO (क्योंकि AC का मध्यबिंदु O है)

BO = DO (क्योंकि BD का मध्यबिंदु O है)

∠AOB = ∠COD (सम्मुख कोण)

इसलिए, ΔAOB ≅ΔCOD (SAS प्रमेय)

इसलिए, AB = CD

या, arc AB = arc D ………………(1)

इसी तरह, arc AD = arc BC ………(2)

इन समीकरणों को जोड़ने पर

Arc AB + arc AD = arc CD + arc BC

इसलिए, यह स्पष्ट है कि BD वृत्त को दो बराबर भागों में विभाजित करता है।

इसलिए, BD एक व्यास है

इसी तरह, AC एक व्यास है

अब प्रश्न के भाग (ii) को हल करते हैं।

हमने पहले सिद्ध किया है ΔAOB ≅ δCOD

या, ∠OAB = ∠OCD

या, ∠CAB = ∠ACD

या, AB||DC

इसी तरह, AD||BC को सिद्ध किया जा सकता है

इससे सिद्ध होता है कि ABCD एक समांतर चतुर्भुज है।

∠DAB = ∠DCB (समांतर चतुर्भुज के सम्मुख कोण)

लेकिन ∠DAB + ∠DCB = 180° (चक्रीय चतुर्भुज के सम्मुख कोण पूरक होते हैं)

इसलिए, ∠DAB = 90° = ∠DCB

इसलिए यह सिद्ध होता है कि ABCD एक आयत है।

प्रश्न 8: एक त्रिभुज ABC के कोणों A, B और C के समद्विभाजक उसके परिवृत्त को क्रमश: D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण 90° - `1/2`A, 90° - `1/2`B तथा 90° - `1/2`C हैं।

उत्तर: इस आकृति में वृत्त के अंदर बने त्रिभुज ABC को दिखाया गया है। ∠A, ∠B और ∠C के समद्विभाजक परिवृत्त को क्रमश: D, E और F पर काटते हैं।

निर्माण: DE, EF और FD को मिलाइए

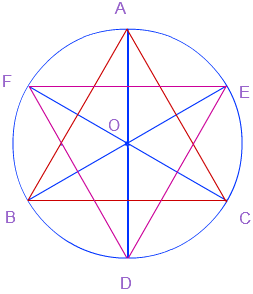
प्रमाण: समान वृत्तखंड के कोण बराबर होते हैं।

इसलिए, ∠FDA = ∠FCA ………………..(1)

∠EDA = ∠EBA ……………………..(2)

इन समीकरणों को जोड़ने पर

∠FDA + ∠EDA = ∠FCA + ∠EBA

`=1/2∠C+1/2∠B`

`=1/2(∠C+∠B)=1/2(180°-∠A)`

`=90°-(∠A)/2`

इसी प्रकार, ∠FED = `(90°-(∠B)/2)`

और, ∠EFD = `(90°-(∠C)/2)`

इसलिए ΔDEF के कोण इस प्रकार हैं

`(90°-(∠A)/2)`, `(90°-(∠B)/2)`, और `(90°-(∠C)/2)`

प्रश्न 9: दो सर्वांगसम वृत्त परस्पर दो बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।

उत्तर: इस आकृति में दो सर्वांगसम वृत्तों को दिखाया गया है जो परस्पर A और B पर प्रतिच्छेद करते हैं। A से गुजरने वाली रेखा वृत्त से P और Q पर मिलती है। अब एक उभयनिष्ठ जीवा AB खींचते हैं।

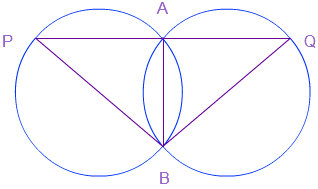
∠APB = ∠AQB (सर्वांगसम वृत्तों में समान जीवा द्वारा बने कोण)

ΔPBQ में

∠AQB = ∠APB

इसलिए, BP = BQ सिद्ध हुआ

प्रश्न 10: किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ΔABC के परिवृत्त पर प्रतिच्छेद करेंगे।

उत्तर: इस आकृति में ΔABC को दिखाया गया है और इस त्रिभुज के परिवृत्त का केंद्र O है। BC का लम्ब समद्विभाजक O से गुजरता है और वृत्त को P पर काटता है। अब OB और OC को मिलाइए

हमें यह सिद्ध करना है कि ∠BAC का समद्विभाजक AP है।

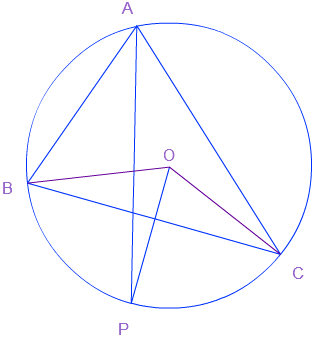
मान लीजिए कि चाप BC द्वारा परिधि पर बना कोण θ है

तब, ∠BOC = 2θ

(चाप द्वारा केंद्र पर बना कोण परिधि पर बने कोण का दोगुना होता है।)

अब ΔBOC में

OB = OC (त्रिज्या)

BC का लम्ब समद्विभाजक OP है।

इसलिए, ∠BOP = ∠COP = θ

चाप CP केंद्र पर θ कोण बनाता है

इसलिए, ∠PAC = `1/2` θ

(चाप द्वारा केंद्र पर बना कोण परिधि पर बने कोण का दोगुना होता है।)

इसका मतलब हुआ कि ∠BAC का समद्विभाजक AP है।