रेखाएँ और कोण

अभ्यास 2

प्रश्न 1: दी गई आकृति में x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।

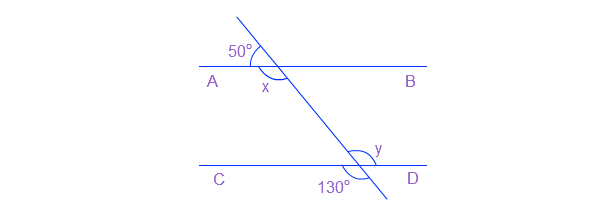
उत्तर: यह स्पष्ट है ∠APM + ∠APN = 180° (कोणों का रैखिक युग्म)

या, ∠APN = 180° - 50° = 130° = x………………..(1)

अब, ∠CQN = ∠DQM (सम्मुख कोण)

या, ∠DQM = 130° = y

हमने देखा कि ∠APN = ∠CQN

इसलिए, तिर्यक रेखा के एक ही ओर बनने वाले संगत कोणों के प्रमेय के अनुसार,

AB║CD

प्रश्न 2: दी गई आकृति में यदि AB || CD, CD || EF और y : z = 3 : 7 है, तो x का मान ज्ञात कीजिए।

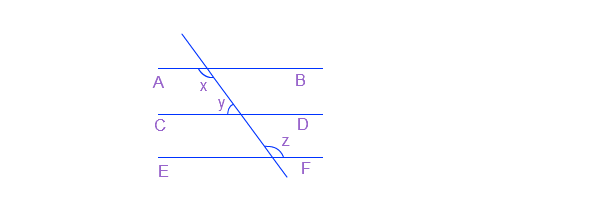
उत्तर: चूँकि CD और EF समांतर हैं

इसलिए, ∠FQP = ∠DPO (संगत कोण)

अब, ∠DPO + ∠CPO = 180°

या, 3x + 7x = 180°

या, 10x = 180°

या, x = 18°

दिए गए अनुपात में x का मान रखने पर

∠DPO = 126° और ∠CPO = 54°

अब, चूँकि AB || CD

इसलिए, ∠DPO = ∠AOP = 126° = x

प्रश्न 3: दी गई आकृति में यदि AB || CD, EF ⊥ CD और ∠GED = 126° है, तो ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए।

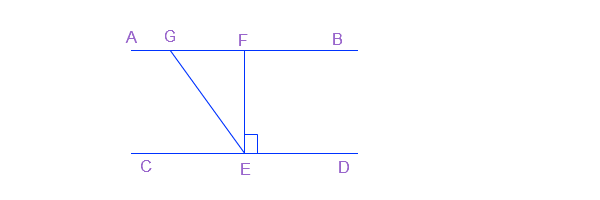
उत्तर: ∠GEF = ∠GED - ∠FED

या, ∠GEF = 126° - 90° = 36°

चूँकि AB || CD,

इसलिए, ∠EFG = ∠FED = 90°

या, ∠FGE = 180°- (90° + 36°) = 54°

अब, ∠AGE + ∠FGE = 180° (कोणों का रैखिक युग्म)

या, ∠AGE = 180° - 54° = 126°

प्रश्न 4: दी गई आकृति में यदि PQ || SR, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS ज्ञात कीजिए।

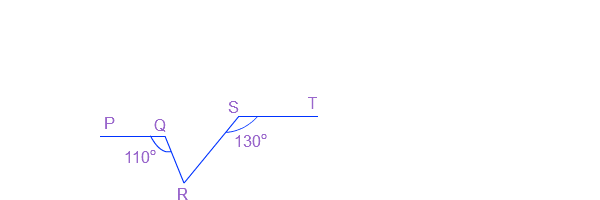
उत्तर: एक रेखा AB जो PQ और ST के समांतर है।

अब, ∠RST + ∠BRS = 180°

और, ∠PQR + ∠ARQ = 180° (तिर्यक रेखा के एक ओर के अंत:कोणों का योग)

इसलिए, ∠BRS = 180° - 130° = 50°

∠ARQ = 180° - 110° = 70°

यह स्पष्ट है ∠ARQ + ∠QRS + ∠BRS = 180°

या, 70° + ∠QRS + 50° = 180°

या, ∠QRS = 60°

प्रश्न 5: दी गई आकृति में यदि AB ||CD, ∠APQ = 50° और ∠PRD = 127° है, तो x और y ज्ञात कीजिए।

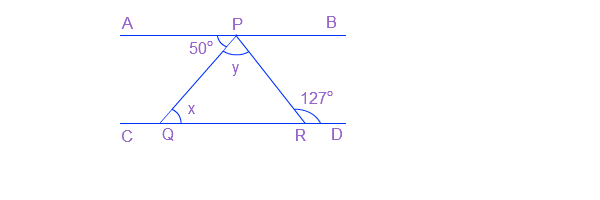
उत्तर: ∠BPR + ∠PRD = 180° (तिर्यक रेखा के एक ओर के अंत:कोणों का योग)

या, ∠BPR = 180° - 127° = 53°

रेखा CD पर, ∠PRD + ∠PRQ = 180°

या, ∠PRQ = 180° - 127° = 53°

रेखा AB पर, ∠APQ + ∠QPR + ∠BPR = 180°

या, ∠QPR = 180° - (50° + 53°) = 77°

ΔPQR में, ∠PQR + ∠QPR + ∠PRQ = 180° (त्रिभुज के तीनों कोणों का योग)

या, ∠PQR = 180° - (77° + 53°) = 50°

या, x = 50° या y = 77°

प्रश्न 6: दी गई आकृति में PQ और RS दो दर्पण हैं जो एक दूसरे के समांतर रखे गए हैं। एक आपतन किरण AB, दर्पण PQ से B पर टकराती है और परावर्तित किरण पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुन: CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB || CD है।

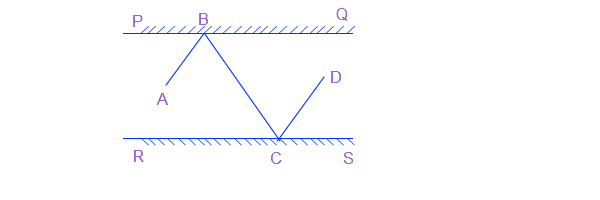
उत्तर: प्रकाश के परावर्तन के नियम के अनुसार, आपतन का कोण और परावर्तन के कोण बराबर होते हैं।

दर्पण PQ के लिए:

आपतन का कोण i = ∠ABP

और परावर्तन का कोण r = ∠QBC

दर्पण RS के लिए:

आपतन का कोण i = ∠BCR

और परावर्तन का कोण r = ∠SCD

AB || CD सिद्ध करने के लिए हमें यह पता करना होगा कि ∠ABC = ∠BCD है या नहीं

रेखा PQ पर:

∠ABP + ∠ABC + ∠QBC = 180°

या, i + ∠ABC + r = 180°

या, i + i + ∠ABC = 180° …………(1)

रेखा RS पर:

i + i + ∠BCD = 180° …………..(2)

प्रश्न के अनुसार PQ ||RS

इसलिए, ∠QBC = ∠BCR (एकांतर कोण)

दोनों दर्पणों के लिए आपतन के कोण बराबर हैं।

इस बात को समीकरण (1) और (2) से मिलाने पर:

∠ABC = ∠BCD

इसलिए, AB||CD सिद्ध हुआ