समांतर चतुर्भुज

अभ्यास 4

Part 1

प्रश्न 7: P और Q क्रमश: त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु हैं तथा R रेखाखंड AP का मध्य बिंदु है। दर्शाइए कि

(a) ar(PRQ) = `1/2` ar(ARC)

उत्तर: ΔAPQ, में AP का मध्यबिंदु R है।

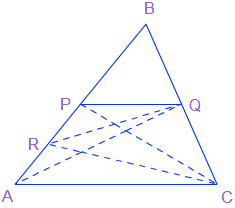
इसलिए, ΔAPQ की एक माध्यिका RQ है।

इसलिए, ar(ΔPRQ) = `1/2` ar(ΔAPQ) ………. (1)

ΔABQ, में AB का मध्यबिंदु P है।

इसलिए, ΔABQ की एक माध्यिका QP है।

इसलिए, ar(ΔAPQ) = `1/2` ar(ΔABQ) ………….(2)

समीकरण (1) और (2) से

ar(ΔPRQ) = `1/2xx1/2` ar(ΔABQ)

= `1/4` ar(ΔABQ) = `1/4xx1/2` ar(ΔABC)

(चूँकि ΔABC की एक माध्यिका AQ है)

इसलिए, ar(ΔPRQ) = `1/8` ar(ΔABC) …………..(3)

अब, ar(ΔARC) = `1/2` ar(ΔAPC)

(चूँकि ΔAPC की एक माध्यिका CR है।)

= `1/2xx1/2` ar(ΔABC)

(चूँकि ΔABC की एक माध्यिका CP है)

इसलिए, ar(ΔARC) = `1/4` ar(ΔABC) ……………(4)

समीकरण (3) से

ar(ΔPRQ) = `1/8` ar(ΔABC)

= `1/2` × (`1/4` ar(ΔABC))

= `1/2` ar(ΔARC) (समीकरण (4) से)

इसलिए, ar(ΔPRQ) = `1/2` ar(ΔARC)

(b) ar(RQC) = `3/8` ar(ABC)

उत्तर: ΔRBC की एक माध्यिका PQ है

इसलिए, ar(RQC) = ar(RBQ)

= ar(PRQ) + ar(BPQ)

= `1/8` ar(ABC) + ar(BPQ) (प्रश्न (a) के समीकरण (3) से)

= `1/8` ar(ABC) + `1/2` ar(PBC) (चूँकि BPC की एक माध्यिका PQ है)

`=1/8` ar(ABC) + `1/2xx1/2` ar(ABC) (चूँकि ABC की एक माध्यिका CP है)

`=1/8` ar(ABC) + `1/4` ar(ABC)

इसलिए, ar(RQC) = `3/8` ar(ABC)

(c) ar(PBQ) = ar(ARC)

उत्तर: ABQ की एक माध्यिका QP है

इसलिए, ar(PBQ) = `1/2` ar(ABQ)

`=1/2xx1/2` ar(ABC) (चूँकि ABC की एक माध्यिका AQ है)

`=1/4` ar(ABC) = ar(ARC) (प्रश्न (a) के समीकरण (4) से)

इसलिए, ar(PBQ) = ar(ARC)

प्रश्न 8: इस आकृति में ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमश: भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखंड AC ⊥ DE भुजा BC को बिंदु Y पर मिलता है। दर्शाइए कि

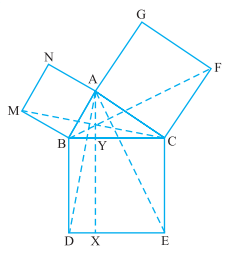
(a) ΔMBC ≅ ΔABD

उत्तर: MB = AB (एक वर्ग की भुजाएँ)

BC = BD (एक वर्ग की भुजाएँ)

∠MBA = ∠DBC = 90° (वर्ग के कोण)

इसलिए, ∠MBA + ∠ABC = ∠DBC + ∠ABC

इसलिए, ∠MBC = ∠ABD

इसलिए, ΔMBC ≅ ΔABD (SAS प्रमेय)

(b) ar(BYXD) = 2 ar(MBC)

उत्तर: चतुर्भुज BYXD और ΔABD एक ही आधार BD पर और समांतर भुजाओं BD और AX के बीच बने हैं

इसलिए, ar(ΔABD) = `1/2` ar(BYXD)

पिछ्ले प्रश्न में सिद्ध हुआ था ΔMBC ≅ ΔABD

इसलिए, ar(ΔMBC) = `1/2` ar(BYXD)

या, ar(BYXD) = 2 ar(ΔMBC)

(c) ΔFCB ≅ ΔACE

उत्तर: FC = AC (एक वर्ग की भुजाएँ)

CB = CE (एक वर्ग की भुजाएँ)

∠ACF = ∠BCE = 90°

इसलिए, ∠ACF + ∠ACB = ∠BCE + ∠ACB

या, ∠FCB = ∠ACE

इसलिए, ΔFCB ≅ ΔACE

(d) ar(CYXE) = 2 ar(FCB)

उत्तर: CYXE और ΔACE एक ही आधार CE पर और समांतर रेखाओं AX और CE के बीच बने हैं

इसलिए, ar(CYXE) = 2 ar(ACE)

पिछले प्रश्न में हमने सिद्ध किया था ΔACE ≅ ΔFCB

इसलिए, ar(CYXE) = 2 ar(FCB)

(e) ar(CYXE) = ar(ACFG)

उत्तर: ACFG Δ FCB एक ही आधार FC पर और समांतर रेखाओं GB और FC के बीच बने हैं।

या, ar(ACFG) = 2 ar(FCB)

पिछले प्रश्न में हमने सिद्ध किया था ar(CYXE) = 2 ar(FCB)

इसलिए, ar(CYXE) = ar(ACFG)

(f) ar(BCED) = ar(ABMN) + ar(ACFG)

उत्तर: ar(BCED) = BC²

ar(ACFG) = AC²

ar(ABMN) = BA²

यहाँ पर, BC कर्ण है, और AC तथा BC समकोण त्रिभुज ABC की दो अन्य भुजाएँ हैं

पाइथागोरस प्रमेय के अनुसार,

`h^2=p^2+b^2`

इसलिए, ar(BCED) = ar(ABMN) + ar(ACFG)