समांतर चतुर्भुज

अभ्यास 4

Part 1

प्रश्न 1: समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।

उत्तर: इस आकृति में, ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है। दोनों एक ही आधार DC पर बने हुए हैं।

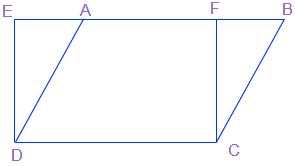
समांतर चतुर्भुज की ऊँचाई= FC

AB = DC (समांतर चतुर्भुज की सम्मुख भुजाएँ)

EF = DC (आयत की सम्मुख भुजाएँ)

इन दो समीकरणों से यह साफ है कि

EF = DC

यानि EA = FB

ABCD का परिमाप= AB + BC + CD + AD

EFCD का परिमाप = EF + FC + CD + ED

= AB + CD + FC + ED

ΔEAD में

AD > ED (कर्ण सबसे लंबी भुजा होती है)

ΔFBC में

BC > FC (कर्ण सबसे लंबी भुजा होती है)

इसलिए, AB + CD + BC + AD > AB + CD + FC + ED

इससे यह सिद्ध होता है कि एक ही आधार पर बने समांतर चतुर्भुज और आयत में से समांतर चतुर्भुज का परिमाप अधिक होता है।

प्रश्न 2: इस आकृति में भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD = DE = EC है। दर्शाइए कि ar(ABD) = ar(ADE) = ar(AEC) है।

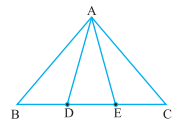
क्या आप अब इस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की ‘भूमिका’ में छोड़ दिया था कि “क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है”?

उत्तर: ΔABD, ΔADE और ΔAEC इन सबकी ऊँचाई = h

BD = DE = EC (दिया गया है)

इसलिए आधार समान हैं

इसलिए हर त्रिभुज का क्षेत्रफल = `1/2xx\h\xxb`

इसलिए, ar(ABD) = ar(ADE) = ar(AEC) सिद्ध हुआ

प्रश्न 3: इस आकृति में ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar(ADE) = ar(BCF) है।

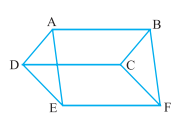
उत्तर: ΔADE और Δ BCF में

AE = BF (समांतर चतुर्भुज ABFE की सम्मुख भुजाएँ)

AD = BC (समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)

DE = CF (समांतर चतुर्भुज DCFE की सम्मुख भुजाएँ)

इसलिए SSS प्रमेय के अनुसार

ΔADE ≅ Δ BCF

या, ar(ΔADE) = ar(Δ BCF) सिद्ध हुआ

प्रश्न 4: इस आकृति में ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है तो दर्शाइए कि ar(BPC) = ar(DPQ) है। (संकेत: AC को मिलाइए)

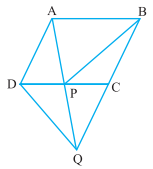
उत्तर: AD = CQ (दिया गया है)

AD = BC (समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ)

इसलिए, AD = CQ = BC

ar(ΔQAC) = ar(ΔQDC)

(एक ही आधार QC और समांतर रेखाओं DA और QC के बीच के त्रिभुज)

दोनों तरफ से ΔQPC घटाने पर

ar(ΔQAC - ΔQPC) = ar(ΔQDC - ΔQPC)

= ar(ΔAPC) = ar(ΔDPQ) ………..(1)

अब, ar(ΔPAC) = ar(ΔPBC) ………..(2)

(एक ही आधार PC समांतर रेखाओं AB और PC के बीच के त्रिभुज)

समीकरण (1) और (2) से

ar(ΔBPC) = ar(ΔDPQ) PROVED